Новости
19.09.2023
Книга «Прикладные структуры данных и алгоритмы. Прокачиваем навыки»
- студент-информатик, который нуждается в простом и понятном ресурсе для изучения структур данных и алгоритмов. Эта книга станет хорошим дополнением к любому классическому учебнику, которым вы пользуетесь;
- начинающий разработчик, который знаком с азами программирования, но хочет изучить основы компьютерных наук, чтобы писать более качественный код и расширить свои знания в этой области;
- программист-самоучка, который никогда не изучал информатику формально (или разработчик, который ее изучал, но уже все забыл!), но хочет использовать мощь структур данных и алгоритмов для написания более качественного и масштабируемого кода.
Кем бы вы ни были, я постарался написать книгу так, чтобы она была доступна для понимания людям с любым уровнем подготовки.
О да! Нотация «О большое»
Ранее мы с вами говорили о том, что основной фактор, определяющий эффективность алгоритма, — это количество выполняемых им шагов.
Но мы не можем просто сказать, что один алгоритм состоит из 22 шагов, а другой — из 400, потому что количество выполняемых алгоритмом шагов не может быть сведено к конкретному числу. Возьмем, к примеру, линейный поиск. Количество шагов этого алгоритма зависит от числа элементов в массиве. Если массив содержит 22 элемента, алгоритм линейного поиска состоит из 22 шагов, а если 400 — то из 400 шагов.
Поэтому, чтобы количественно оценить эффективность этого алгоритма, мы можем сказать, что для выполнения линейного поиска в массиве из N элементов нужно N шагов. То есть если в массиве содержится N элементов, линейный поиск будет состоять из N шагов. Но такой способ выражения эффективности довольно громоздкий.
Чтобы облегчить обсуждение временной сложности, программисты позаимствовали из мира математики концепцию, благодаря которой можно лаконично и согласованно описывать эффективность структур данных и алгоритмов. Формальный способ выражения этих концепций называется нотацией «О большое» (Big O) или О-нотацией и позволяет легко оценивать эффективность любого алгоритма и сообщать о ней другим.
Разобравшись с О-нотацией, вы научитесь описывать алгоритмы согласованно и лаконично, как профессионалы.
Хотя О-нотация пришла из мира математики, я собираюсь обойтись без сложной терминологии и объяснить ее суть в контексте компьютерных наук. Мы начнем с малого: познакомимся с этой концепцией поверхностно, постепенно углубляясь в ее изучение на протяжении этой и следующих трех глав. Тема несложная, но еще проще ее будет усвоить по частям.
«O большое»: количество шагов при наличии N элементов
Согласованность О-нотации обусловлена особым способом подсчета количества шагов алгоритма. Сначала давайте попробуем оценить с ее помощью эффективность алгоритма линейного поиска.
В худшем случае количество шагов линейного поиска будет равно количеству элементов в массиве. Как мы уже говорили, линейный поиск в массиве из N элементов может потребовать до N шагов. С помощью О-нотации это можно выразить так: O(N).
Некоторые произносят это как «О большое от эн» или «сложность порядка N». Но я предпочитаю говорить просто: «О от эн».
Эта запись выражает ответ на ключевой вопрос: сколько шагов будет выполнять алгоритм при наличии N элементов данных? Выучите это предложение наизусть, потому что именно это определение О-нотации мы будем использовать на протяжении всей оставшейся части книги.
Ответ на ключевой вопрос в этом выражении заключен в круглые скобки. Запись O(N) говорит о том, что алгоритм будет выполнять N шагов.
Теперь давайте рассмотрим выражение временной сложности с помощью О-нотации на примере того же линейного поиска. Сначала мы задаем ключевой вопрос: если в массиве N элементов данных, сколько шагов нужно для выполнения линейного поиска? Мы знаем, что на выполнение такого поиска уйдет N шагов, поэтому выражаем ответ так: O(N). Для справки, O(N) еще называют алгоритмом с линейной временной сложностью или выполняемым за линейное время.
Сравним все это с выражением эффективности чтения из стандартного массива через О-нотацию. Как вы узнали из главы 1, на чтение из массива, вне зависимости от его размера, уходит всего шаг. Чтобы выразить сложность этого алгоритма в О-нотации, мы снова зададим ключевой вопрос: если в массиве N элементов данных, сколько шагов нужно для чтения из него? Ответ: один шаг, поэтому мы можем выразить сложность этого алгоритма так: O(1) (произносится как «О от единицы»).
Случай с O(1) довольно интересен: несмотря на то что ключевой вопрос основан на терминах N («Сколько шагов будет выполнять алгоритм при N элементах данных?»), ответ никак не относится к N. В этом и суть: сколько бы элементов ни было в массиве, чтение из него всегда требует только одного шага.
И именно поэтому алгоритм со сложностью O(1) считается «самым быстрым». Даже по мере увеличения объема данных он не выполняет никаких дополнительных шагов, то есть всегда выполняет одно и то же их количество вне зависимости от значения N. Алгоритм O(1) еще называют алгоритмом с постоянной временной сложностью или выполняемым за постоянное (константное) время.
А где же математика?
Как я уже говорил, в этой книге я постарался объяснить тему О-нотации максимально просто. Но сделать это можно и другими способами. Если вы проходили формальный курс обучения, то наверняка знакомы с этой концепцией с математической точки зрения. О-нотация была позаимствована из мира математики, поэтому для ее описания часто используют математические термины. И тогда можно услышать такие выражения, как «“О” большое описывает верхнюю границу скорости роста функции» или «если функция g(x) растет не быстрее функции f(x), то g является элементом O(f)». Все эти фразы либо имеют смысл, либо нет — все зависит от вашего уровня подготовки. В своей книге я постарался объяснить эту тему так, чтобы ее могли понять даже те, кто далек от математики.
Если хотите углубиться в математические основы О-нотации, прочтите книгу Introduction to Algorithms Томаса Х. Кормена, Чарльза И. Лейзерсона, Рональда Л. Ривеста и Клиффорда Штайна или статью Джастина Абрамса: justin.abrah.ms/computer-science/understanding-big-o-formal-definition.html.
Суть О-нотации
Теперь, когда мы познакомились с O(N) и O(1), мы начинаем понимать, что О-нотация не просто описывает количество шагов, которые выполняет алгоритм, например, с жестким числом, таким как 22 или 400. Это скорее ответ на поставленный ранее ключевой вопрос: сколько шагов будет выполнять алгоритм при наличии N элементов данных?
Но суть О-нотации не только в этом.
Допустим, у нас есть алгоритм, который всегда выполняет три шага вне зависимости от количества данных. То есть при наличии N элементов алгоритм всегда состоит из трех шагов. Как это выразить с помощью О-нотации?
Исходя из всего, что вы узнали, вы можете ответить: O(3).
Но правильный ответ — O(1). Сейчас я объясню, почему.
Хотя с помощью О-нотации действительно можно выразить количество шагов алгоритма при наличии N элементов данных, это определение не затрагивает нечто более глубокое, «суть» этой нотации.
О-нотация может ответить на вопрос: «Как изменяется производительность алгоритма по мере увеличения объема данных?»
Она не просто говорит нам, сколько шагов выполняет алгоритм, но и показывает, как число шагов увеличивается по мере изменения объема данных.
В этом случае нам все равно, чему равна временная сложность алгоритма — O(1) или O(3), ведь она никак не зависит от объема данных, так как число шагов остается постоянным. По сути, оба алгоритма относятся к одному типу, ведь ни в первом, ни во втором алгоритме число шагов не меняется при изменении количества данных. Поэтому для нас они одинаковы.
В свою очередь, алгоритм со сложностью O(N) относится к другому типу, так как на его производительность влияет увеличение объема данных. Если конкретнее, то вместе с объемом данных увеличивается и количество шагов алгоритма. Именно об этом нам сообщает запись O(N). Она отражает пропорциональную зависимость между объемом данных и эффективностью алгоритма: описывает то, как растет количество шагов по мере увеличения объема данных.
Рассмотрим графики эффективности алгоритмов этих двух типов:
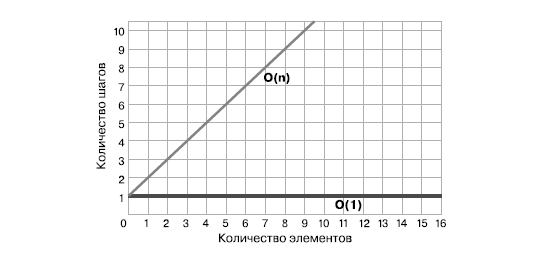
Обратите внимание, что график O(N) образует диагональную линию. Это связано с тем, что при каждом добавлении фрагмента данных в алгоритм добавляется один шаг: чем больше данных, тем больше шагов выполняет алгоритм.
Теперь посмотрим на график O(1), который образует горизонтальную линию. Так происходит потому, что число шагов остается неизменным вне зависимости от количества данных.
Погружение в суть О-нотации
Чтобы осознать истинную суть О-нотации, давайте немного углубимся в эту тему. Допустим, у нас есть алгоритм с постоянной сложностью, который всегда выполняет 100 шагов вне зависимости от количества данных. Насколько он эффективен по сравнению с алгоритмом O(N)?
Взгляните на следующий график:
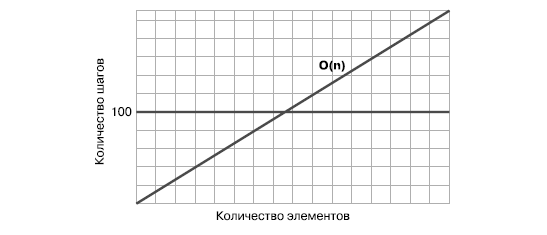
Мы видим, что при работе с набором данных, где меньше 100 элементов, алгоритм O(N) выполняет меньше шагов, чем 100-шаговый алгоритм O(1). В точке, соответствующей 100 элементам, графики пересекаются, потому что при таком объеме данных оба алгоритма выполняют одинаковое количество шагов — 100. Но суть в другом: при работе с массивами, где больше 100 элементов, алгоритм O(N) выполняет больше шагов, чем O(1).
Поскольку всегда есть некая точка перелома, по достижении которой алгоритм O(N) начинает выполнять больше шагов, вплоть до бесконечности, в целом он считается менее эффективным, чем O(1), вне зависимости от того, сколько шагов выполняет последний.
То же верно и для алгоритма O(1), который всегда выполняет миллион шагов. В процессе роста объема данных неизбежно будет достигнута точка, после которой O(N) станет менее эффективным, чем O(1).
Один алгоритм, разные сценарии
Как вы уже знаете, сложность алгоритма линейного поиска не всегда O(N). Если искомый элемент находится в последней ячейке массива, то для его нахождения действительно нужно N шагов. Но когда элемент в первой ячейке, алгоритм линейного поиска найдет его всего за шаг. Этот случай линейного поиска будет выглядеть так: O(1). Если бы мы захотели максимально полно описать эффективность этого алгоритма, то сказали бы, что сложность линейного поиска равна O(1) в лучшем случае и O(N) — в худшем.
Хотя О-нотация эффективно описывает как лучший, так и худший сценарии для этого алгоритма, приводимые оценки обычно относятся к последнему, если не указано иное. Вот почему линейный поиск часто описывается как алгоритм со сложностью O(N), несмотря на то что в лучшем случае она может быть равна O(1).
Все из-за того, что такой «пессимистический» подход довольно полезен, поскольку точное знание того, насколько неэффективным может оказаться алгоритм, готовит к худшему и влияет на наше итоговое решение.
Алгоритм третьего типа
В прошлой главе вы узнали, что двоичный поиск в упорядоченном массиве выполняется намного быстрее, чем линейный. Теперь посмотрим, как можно описать сложность двоичного поиска с помощью О-нотации.
Мы не можем использовать запись O(1), так как число шагов алгоритма увеличивается по мере роста объема данных. Но этот алгоритм не вписывается и в категорию O(N), ведь число его шагов намного меньше, чем N элементов данных. Как мы видели, для выполнения двоичного поиска в массиве из 100 элементов нужно всего семь шагов.
Поэтому сложность алгоритма двоичного поиска находится где-то между O(1) и O(N). Так какова же она?
Временная сложность двоичного поиска выражается с помощью О-нотации так: O(log N).
Я произношу это как «О от логарифма эн». Алгоритмы такого типа обладают логарифмической временной сложностью, то есть выполняются за логарифмическое время.
Проще говоря, O(log N) описывает алгоритм, число шагов в котором увеличивается на единицу при каждом удвоении объема данных. Как было сказано ранее, в случае с двоичным поиском дело обстоит именно так. Чуть позже вы поймете, почему мы используем именно выражение O(log N), но сначала закрепим пройденный материал.
Запишем рассмотренные типы алгоритмов в порядке убывания эффективности:
O(1);
O(log N);
O(N).
Теперь посмотрим, как это выражается графически:
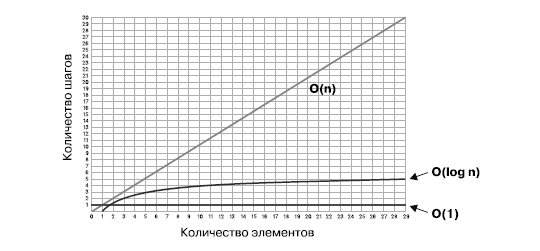
Обратите внимание, что кривая O(log N) растет очень медленно. Это делает алгоритм менее эффективным, чем O(1), но более эффективным, чем O(N).
Чтобы понять, почему сложность этого алгоритма выражается как O(log N), нужно познакомиться с понятием логарифма. Если с этой темой вы знакомы, можете пропустить следующий раздел.
Логарифмы
Давайте выясним, почему сложность таких алгоритмов, как двоичный поиск, записывается как O(log N). Что вообще означает log?
Log — это сокращение от слова logarithm (логарифм). Первым делом важно усвоить то, что логарифмы никак не связаны с алгоритмами, несмотря на схожесть этих слов.
Нахождение логарифма — это действие, обратное возведению в степень.
Например:
23 равнозначно 2 × 2 × 2, что равно 8.
Вычисление log2 8 — обратное действие. Здесь нужно определить, сколько раз нужно умножить число 2 само на себя, чтобы получить 8.
Для этого 2 нужно умножить само на себя 3 раза, поэтому log2 8 = 3.
Вот еще один пример:
26 равнозначно 2 × 2 × 2 × 2 × 2 × 2 = 64.
Так как для получения 64 нам пришлось умножить число 2 само на себя шесть раз, log2 64 = 6.
Выше приведено классическое объяснение логарифмов, но я предпочитаю использовать другое, более простое для понимания, особенно в контексте О-нотации.
Вот как еще можно подойти к вычислению log2 8: если бы мы продолжали делить 8 на 2 вплоть до получения 1, сколько двоек оказалось бы в нашем выражении?
8 / 2 / 2 / 2 = 1.
Иначе говоря, сколько раз нам нужно разделить 8 пополам, чтобы получить 1? В данном примере — три. Поэтому log2 8 = 3.
Точно так же можно вычислить и log2 64: сколько раз нужно разделить 64 пополам, чтобы получить 1?
64 / 2 / 2 / 2 / 2 / 2 / 2 = 1.
Поскольку у нас получилось шесть двоек, log2 64 = 6.
Теперь, когда вы узнали, что такое логарифмы, запись O(log N) обретет для вас смысл.
Значение выражения O(log N)
Вернемся к О-нотации. В мире информатики под выражением O(log N) подразумевается выражение O(log2 N). Мы просто опускаем эту маленькую двойку для удобства.
Напомню, что О-нотация помогает узнать, сколько шагов будет выполнять алгоритм при наличии N элементов данных.
Запись O(log N) означает, что при наличии N элементов данных алгоритм будет выполнять log2 N шагов. Если элементов 8, то алгоритм будет состоять из трех шагов, так как log2 8 = 3.
Другими словами, если мы будем последовательно делить 8 элементов пополам, нам понадобится три шага, чтобы получить 1 элемент.
Именно это происходит с бинарным поиском. Чтобы найти конкретный элемент, мы последовательно делим количество ячеек массива пополам, пока не сузим диапазон до предела.
Проще говоря: O(log N) означает, что алгоритм выполняет столько шагов, сколько нужно для того, чтобы остаться с одним элементом в результате последовательного деления объема данных пополам.
В следующей таблице вы можете увидеть поразительную разницу в эффективности между алгоритмами O(N) и O(log N):
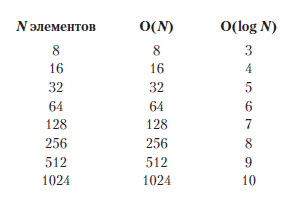
В случае с алгоритмом O(N) число шагов увеличивается на единицу при каждом добавлении элемента, а в случае с алгоритмом O(log N) — при каждом удвоении всего объема данных.
В следующих главах вы познакомитесь с алгоритмами, которые не попадают ни в одну из рассмотренных нами трех категорий. А пока применим полученные знания к нескольким примерам кода.
Практические примеры
Вот типичный код на Python для вывода на экран всех элементов списка:
things = ['apples', 'baboons', 'cribs', 'dulcimers']
for thing in things:
print("Here's a thing: %s" % thing)
Как описать сложность этого алгоритма с помощью О-нотации?
Во-первых, нужно понять, что мы имеем дело с примером алгоритма. По сути, любой код, который делает хоть что-то, — это уже алгоритм, некий способ выполнения определенной задачи. В нашем случае задача — вывод на экран всех элементов списка. Для ее выполнения мы используем такой алгоритм, как цикл for с оператором print.
Теперь нужно проанализировать, сколько шагов выполняет этот алгоритм. В нашем примере основная часть алгоритма — цикл for — состоит из четырех шагов, потому что в списке содержится четыре элемента, и каждый из них выводится на экран один раз.
Но количество шагов может меняться. Если бы наш список содержал десять элементов, цикл for выполнял бы десять шагов. Так как этот цикл for выполняет столько шагов, сколько элементов в списке, мы можем сказать, что сложность этого алгоритма равна O(N).
Следующий пример — простой алгоритм на основе Python для определения того, является ли число простым:
def is_prime(number):
for i in range(2, number):
if number % i == 0:
return False
return True
Этот код принимает в качестве аргумента число number и запускает цикл for, в котором делит переданное значение на каждое целое число от 2 до number и проверяет результат на наличие остатка. Если остатка нет, значит, число не простое, и код возвращает False. Если number делится с остатком на все числа диапазона, значит, оно простое, и код возвращает True.
Цель в этом примере немного отличается от тех, что были ранее. Раньше нас интересовало количество шагов алгоритма при наличии в массиве N элементов данных. Здесь мы имеем дело не с массивом, а с числом, которое передаем функции, и от величины этого числа зависит то, сколько раз будет выполняться цикл.
Ключевой вопрос в этом случае будет следующим: «Сколько шагов будет выполнять алгоритм при передаче числа N?»
Если мы передадим функции is_prime число 7, то цикл for будет выполняться примерно семь раз (технически он выполняется пять раз: диапазон чисел, на которые производится деление, начинается с 2 и заканчивается перед заданным числом). В случае с числом 101 цикл выполняется примерно 101 раз. Поскольку количество шагов алгоритма увеличивается на один, когда повышается на единицу величина переданного функции числа, мы имеем дело с классическим примером алгоритма со сложностью O(N).
Опять же, ключевой вопрос здесь относится к N другого типа, ведь нас интересует число, а не массив. В следующих главах мы подробнее поговорим об определении разных типов N.
Выводы
О-нотация дает нам согласованную систему для сравнения любых алгоритмов. С ее помощью мы можем исследовать сценарии из реальной жизни, структуры данных и алгоритмы, чтобы выбрать те, которые позволяют сделать наш код максимально быстрым и способным справляться с большими нагрузками.
В следующей главе мы разберем реальный пример ускорения выполнения кода благодаря использованию О-нотации.
Более подробно с книгой можно ознакомиться на сайте издательства.





Комментарии: 0
Пока нет комментариев