Новости

Машинное обучение для регрессии

Выполнив первоначальный анализ данных, мы готовы обучать модель. Проблема, которую мы решаем, — это задача регрессии: цель состоит в том, чтобы предсказать число‚ а именно цену автомобиля. Для этого проекта мы будем использовать простейшую регрессионную модель: линейную регрессию.

2.3.1. Линейная регрессия

Чтобы спрогнозировать цену автомобиля, нам нужно использовать какую-то модель машинного обучения. В нашем случае мы будем использовать линейную регрессию, которую реализуем самостоятельно. Как правило, вручную это не делается‚ и подобную работу выполняет какая-либо библиотека. Однако в этой главе мы хотим показать, что внутри таких фреймворков нет ничего волшебного: это просто код. Линейная регрессия — идеальная модель, поскольку она относительно проста и может быть реализована с помощью всего нескольких строк кода NumPy.

Для начала разберемся, как работает линейная регрессия. Как мы знаем из главы 1, модель контролируемого машинного обучения имеет определенную форму:

y ≈ g(X).

Это матричная форма. X — матрица, где признаки наблюдений являются строками матрицы, а y — вектор со значениями, которые требуется спрогнозировать.

Эти матрицы и векторы могут запутывать, так что сделаем шаг назад и рассмотрим, что происходит с одним наблюдением x_i и значением y_i, которое мы хотим спрогнозировать. Индекс i здесь означает, что это номер наблюдения i, одно из m наблюдений, которые содержатся в нашем обучающем наборе данных.

Тогда для этого единственного наблюдения предыдущая формула выглядит следующим образом:

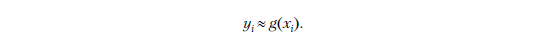
Если у нас есть n признаков, то наш вектор x_i является n-мерным, поэтому он содержит n компонентов:

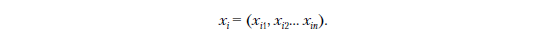
Поскольку он имеет n компонентов, мы можем записать функцию g как функцию с n параметрами, что совпадает с предыдущей формулой:

В нашем случае у нас в обучающем наборе данных 7150 автомобилей. Это означает, что m = 7150, а i может быть любым числом от 0 до 7149. Для i = 10, например, мы получим такой автомобиль:

make                                  rolls-royce
model                      phantom_drophead_coupe
year                                         2015
engine_fuel_type      premium_unleaded_(required)
engine_hp                                     453
engine_cylinders                               12
transmission_type                       automatic
driven_wheels                    rear_wheel_drive
number_of_doors                                 2
market_category         exotic,luxury,performance
vehicle_size                                large
vehicle_style                         convertible
highway_mpg                                    19
city_mpg                                       11
popularity                                     86
msrp                                       479775

Выберем несколько числовых признаков и пока проигнорируем остальные. Мы можем начать с лошадиных сил, миль на галлон по городу и популярности:

engine_hp          453
city_mpg            11
popularity          86

Затем присвоим эти признаки x_i1, x_i2 и x_i3 соответственно. Таким образом, мы получаем вектор признаков xi с тремя компонентами:

Чтобы лучше все понять описываемое, мы можем перевести эту математическую нотацию на Python. В нашем случае функция g имеет следующую сигнатуру:

def g(xi):
    # xi — это список из n элементов
    # делаем что-нибудь с xi
    # вернуть результат
    pass

В этом коде переменная xi — это наш вектор xi. В зависимости от реализации xi может быть списком с n элементами или массивом NumPy, имеющим размер n.

Для автомобиля, описанного ранее, xi представляет собой список из трех элементов:

xi = [453, 11, 86]

Когда мы применяем функцию g к вектору xi, она выдает y_pred в качестве вывода, который является прогнозом g для xi:

y_pred = g(xi)

Мы ожидаем, что прогноз окажется как можно ближе к yi, реальной цене автомобиля.

ПРИМЕЧАНИЕ

Чтобы проиллюстрировать идеи, лежащие в основе математических формул, в этом разделе мы будем использовать Python. Нам не требуется использовать эти фрагменты кода для самого проекта. С другой стороны, запуск данного кода в Jupyter может помочь понять концепции.

Функция g может выглядеть по-разному, и выбор алгоритма машинного обучения определяет способ ее работы.

Если g — модель линейной регрессии, то она получит следующий вид:

Переменные w₀, w₁, w₂… wn служат параметрами модели:
• w₀ — составляющая смещения;
• w₁, w₂… w_n — веса каждого признака x_i1, x_i2… x_in.

Эти параметры точно определяют, как модель должна комбинировать признаки, чтобы прогнозы в итоге получились максимально хорошими. Ничего страшного, если значение этих параметров пока не до конца ясно, поскольку мы рассмотрим их несколько позже.

Чтобы формула была короче, используем обозначение суммы:

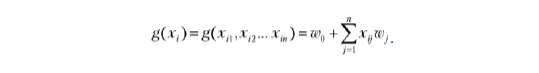
Упражнение 2.2

Для контролируемого обучения мы используем модель машинного обучения для единственного наблюдения y_i ≈ g(x_i). Что такое x_i и y_i в этом проекте?

А. x_i — вектор признаков, содержащий ряд чисел, описывающих объект (автомобиль), а y_i — логарифм цены этого автомобиля.

Б. y_i — вектор признаков‚ содержащий ряд чисел, описывающих объект (автомобиль), а x_i — логарифм цены этого автомобиля.

Указанные веса — это то, что модель усваивает, когда мы ее обучаем. Чтобы лучше понять, как модель использует веса, рассмотрим следующие значения (табл. 2.1).

Итак, если мы захотим перевести эту модель на Python, то она будет выглядеть следующим образом:

w0 = 7.17
#   [w1    w2    w3   ]
w = [0.01, 0.04, 0.002]
n = 3

def linear_regression(xi):
    result = w0
    for j in range(n):
        result = result + xi[j] * w[j]
    return result

Мы помещаем все веса объектов в один список w — точно так же, как мы ранее поступили с xi. Все, что нам теперь нужно сделать, — перебрать эти веса и умножить их на соответствующие значения признаков. Это и будет не чем иным, как прямым переводом предыдущей формулы на Python.

Разобраться в этом достаточно легко. Взгляните еще раз на формулу:

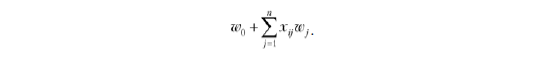
В нашем примере имеются три признака, поэтому n = 3, и мы получаем

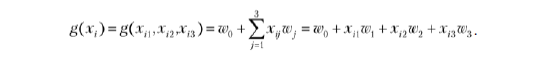
Это именно то, что мы видим в коде

result = w0 + xi[0] * w[0] + xi[1] * w[1] + xi[2] * w[2]

за простым исключением, что индексация в Python начинается с 0, xi1 превращается в xi[0]‚ а w₁ — в w[0].

Теперь посмотрим, что произойдет, когда мы применим модель к нашему наблюдению xi и заменим веса их значениями:

Прогноз, который мы получим для этого наблюдения, будет равен 12,31. Вспомните, что во время предварительной обработки мы применили к нашей целевой переменной y логарифмическое преобразование. Вот почему модель, которую мы обучили на этих данных, также предсказывает логарифм цены. Чтобы отменить преобразование, нам нужно взять экспоненту логарифма. В нашем случае прогноз становится равным 603 000 долларов:

exp(12,31 + 1) = 603 000.

Смещение (7,17) — это значение, которое мы бы получили, если бы ничего не знали об автомобиле; оно служит базовой линией.

Однако мы кое-что знаем об этом автомобиле: мощность, миль на галлон по городу (MPG) и популярность. Это признаки x_i1, x_i2 и x_i3, каждый из которых что-то говорит нам об автомобиле. Мы используем данную информацию для корректировки базовой линии.

Рассмотрим первый признак: лошадиные силы. Вес для этого признака равен 0,01, это значит, для каждой дополнительной единицы лошадиной силы мы корректируем базовую линию, добавляя 0,01. Поскольку у нас в двигателе 453 лошади, мы добавляем 4,53 к базовому показателю: 453 л/c · 0,01 = 4,53.

То же самое происходит и с MPG. Каждая дополнительная миля на галлон увеличивает цену на 0,04, поэтому мы добавляем 0,44: 11 м/г · 0,04 = 0,44.

Наконец мы принимаем во внимание популярность. В нашем примере каждое упоминание в ленте Twitter приводит к увеличению на 0,002. В общей сложности популярность вносит 0,172 в окончательный прогноз.

Именно поэтому мы получаем 12,31, когда сводим все воедино (рис. 2.11).

Теперь вспомним, что на самом деле мы имеем дело с векторами, а не с отдельными числами. Мы знаем, что x_i — это вектор с n компонентами:

Мы также можем объединить все веса в один вектор w:

Фактически мы уже делали это в примере Python, когда помещали все веса в список, который представлял собой вектор размерности 3 с весами для каждого отдельного признака. Вот как выглядят векторы в нашем примере:

Поскольку теперь мы думаем о признаках и весах как о векторах x_i и w соответственно, мы можем заменить сумму элементов этих векторов их скалярным произведением:

Скалярное произведение — это способ умножения двух векторов: мы умножаем соответствующие элементы векторов, после чего суммируем результаты. В приложении В можно найти более подробную информацию об умножении вектора на вектор.

Перевод формулы для скалярного произведения в код прост:

def dot(xi, w):
    n = len(w)
    result = 0.0
    for j in range(n):
    result = result + xi[j] * w[j]
return result

Используя новую нотацию, мы можем переписать все уравнение для линейной регрессии как

где

• w₀ — компонент смещения;
• w — n-мерный вектор весов.

Теперь мы можем использовать новую функцию dot, поэтому функция линейной регрессии в Python становится очень короткой:

def linear_regression(xi):
    return w0 + dot(xi, w)

В качестве альтернативы, если xi и w являются массивами NumPy, мы можем использовать для умножения встроенный метод dot:

def linear_regression(xi):
    return w0 + xi.dot(w)

Чтобы сделать его еще короче, мы можем объединить w0 и w в один (n + 1)-мерный вектор, добавив w₀ к w прямо перед w₁:

Таким образом, мы получаем вектор весов w, состоящий из компонента смещения w₀, за которым следуют веса w₁, w₂,… из исходного вектора весов w.

В Python это проделать очень легко. Если у нас уже есть старые веса в списке w, то нам нужно лишь выполнить следующую операцию:

w = [w0] + w

Помните, что оператор + в Python объединяет списки, поэтому [1] + [2, 3, 4] создаст новый список из четырех элементов: [1, 2, 3, 4]. В нашем случае w уже является списком, поэтому мы создаем новый w с одним дополнительным элементом в начале: w0.

Поскольку теперь w становится (n + 1)-мерным вектором, нам также нужно настроить вектор объектов x_i так, чтобы скалярное произведение по-прежнему работало. Это легко сделать, добавив фиктивный признак x_i0, который всегда принимает значение 1. Затем мы добавим этот новый фиктивный признак к x_i прямо перед x_i1:

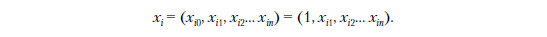
Или в коде:

xi = [1] + xi

Мы создаем новый список xi с 1 в качестве первого элемента, за которым следуют все элементы из старого списка xi.

С помощью этих модификаций мы можем выразить модель как скалярное произведение между новым x_i и новым w:

В коде это выразить просто:

w0 = 7,17
w = [0.01, 0.04, 0.002]
w = [w0] + w

def linear_regression(xi):
    xi = [1] + xi
    return dot(xi, w)

Эти формулы для линейных регрессий эквивалентны, поскольку первый признак нового x_i равен 1, поэтому, умножая первый компонент x_i на первый компонент w, мы получаем компонент смещения, поскольку w₀ × 1 = w₀.

Теперь мы готовы вернуться к общей картине и поговорить о матричной форме. В данных содержится много наблюдений, и x_i — одно из них. Таким образом, у нас есть m векторов признаков x₁, x₂, ..., x_i, ..., x_m, и каждый из этих векторов состоит из n + 1 признаков:

Мы можем сложить эти векторы вместе в виде строк матрицы. Назовем эту матрицу X (рис. 2.12).

Посмотрим, как это выглядит в коде. Мы можем взять несколько строк из обучающего набора данных, например первую, вторую и десятую:

x1  = [1, 148, 24, 1385]
x2  = [1, 132, 25, 2031]
x10 = [1, 453, 11, 86]

Теперь объединим строки в другой список:

X = [x1, x2, x10]

Список X теперь содержит три списка. Мы можем думать об этом как о матрице 3 × 4 — матрице с тремя строками и четырьмя столбцами:

X = [[1, 148, 24, 1385],
     [1, 132, 25, 2031],
     [1, 453, 11, 86]]

Каждый столбец этой матрицы представляет собой признак:
1) первый столбец — фиктивный признак с «1»;
2) второй столбец — мощность двигателя;
3) третий — MPG в городе;
4) и последний — популярность, или количество упоминаний в Twitter.

Вы уже знаете, что, для того чтобы сделать прогноз для одного вектора признаков, нам нужно вычислить скалярное произведение этого вектора признаков и вектора весов. Теперь у нас есть матрица X, которая в Python представляет собой список векторов признаков. Чтобы сделать прогнозы для всех строк матрицы, мы можем просто перебрать все строки X и вычислить скалярное произведение:

predictions = []

for xi in X:
    pred = dot(xi, w)
    predictions.append(pred)

В линейной алгебре это умножение матрицы на вектор: мы умножаем матрицу X на вектор w. Формула для линейной регрессии превращается в

Результатом будет массив с прогнозами для каждой строки X. Более подробную информацию о матрично-векторном умножении можно найти в приложении В.

При такой формулировке матрицы код для применения линейной регрессии для составления прогнозов становится очень простым, как и перевод на NumPy:

predictions = X.dot(w)

Упражнение 2.3

Когда мы умножаем матрицу X на вектор весов w, что мы получаем?
А. Вектор y с фактической ценой.
Б. Вектор y с прогнозами цен.
В. Одно число y с прогнозами цен.

2.3.2. Обучающая модель линейной регрессии

До сих пор мы рассматривали только прогнозирование. Чтобы иметь возможность это сделать, нам нужно знать веса w. Как мы их получим?

Мы узнаем веса из данных: используем целевую переменную y, чтобы найти такую w, которая наилучшим образом сочетает в себе признаки X. «Наилучшим образом» в случае линейной регрессии означает, что ошибка между прогнозами g(X) и фактическим целевым значением y сведена к минимуму.

У нас для этого есть несколько способов. Мы используем нормальное уравнение, которое служит самым простым методом реализации. Весовой вектор w может быть вычислен по следующей формуле:

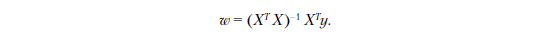
ПРИМЕЧАНИЕ

Выведение нормального уравнения выходит за рамки этой книги. Мы даем некоторое представление о том, как оно работает, в приложении В, но более подробно познакомиться с темой вам поможет учебник по машинному обучению. Книга The Elements of Statistical Learning, 2nd edition Г. Фридмана, Р. Тибширани и Т. Хасти (Friedman, Tibshirani, Hastie) будет весьма полезной на начальном этапе.

Эта математическая часть может напугать или запутать, но ее довольно легко перевести на NumPy:

• X^T — транспонирование X. В NumPy это X.T;

• X^TX — умножение матрицы на матрицу, которое мы можем выполнить с помощью метода dot из NumPy: X.T.dot(X);

• X^–1 — величина, обратная X. Для обращения мы можем использовать функцию np.linalg.inv.

Таким образом, приведенная выше формула превращается непосредственно в

inv(X.T.dot(X)).dot(X.T).dot(y)

Более подробную информацию об этом уравнении можно найти в приложении В.

Чтобы реализовать нормальное уравнение, нам нужно проделать следующее:
1. Создать функцию, которая принимает матрицу X с признаками и вектор y с целью.
2. Добавить фиктивный столбец (признак, который всегда содержит значение 1) в матрицу X.
3. Обучить модель: вычислить веса w, используя нормальное уравнение.
4. Разделить полученный w на смещение w₀ и остальные веса и вернуть их.

Последний шаг — разделение w на компонент смещения и остаток — необязателен и в основном нужен для удобства; в противном случае нам пришлось бы добавлять фиктивный столбец каждый раз, когда мы захотим получить прогноз, вместо того чтобы сделать это один раз во время обучения.

Реализуем все это (листинг 2.2).

С помощью шести строк кода мы внедрили наш первый алгоритм машинного обучения. В ❶ мы создаем вектор, содержащий только единицы, который мы добавляем к матрице X в качестве первого столбца; это фиктивный признак в ❷. Далее мы вычисляем X^TX в ❸ и его обратное значение в ❹ и объединяем их, чтобы вычислить w в ❺. Наконец мы разделяем веса на смещение w₀ и остальные веса w в ❻.

Функция column_stack в NumPy, которую мы использовали для добавления столбца‚ поначалу может смутить, поэтому рассмотрим ее более пристально:

np.column_stack([ones, X])

Она принимает список массивов NumPy, который в нашем случае содержит ones и X, и складывает их (рис. 2.13).

Если разделить веса на компонент смещения и остаток, то формула линейной регрессии для составления прогнозов немного изменится:

Это по-прежнему очень легко перевести на NumPy:

y_pred = w0 + X.dot(w)

Давайте используем ее для нашего проекта!

Более подробно с книгой можно ознакомиться на сайте издательства.