Новости

Протоколы аутентификации

Аутентификация — это метод, с помощью которого процесс проверяет, является ли его собеседник тем, за кого он себя выдает. Проверка подлинности удаленного процесса при активных умышленных попытках проникновения представляет собой на удивление сложную задачу и требует применения сложных протоколов, основанных на криптографии. В данном разделе мы познакомимся с несколькими протоколами аутентификации, которые используются в незащищенных компьютерных сетях.

Следует отметить, что иногда аутентификацию путают с авторизацией. Аутентификация связана с вопросом подлинности процесса, с которым происходит взаимодействие. Авторизация касается того, что этому процессу разрешено делать. Например, клиентский процесс обращается к файловому серверу и говорит: «Я процесс Скотта, и я хочу удалить файл cookbook.old». Файл-сервер должен ответить на два вопроса:

1. Действительно ли это процесс Скотта (аутентификация)?
2. Есть ли у Скотта право на удаление файла cookbook.old (авторизация)?

Только получив однозначный утвердительный ответ на оба вопроса, можно выполнить запрошенное действие. Ключевым является первый вопрос. После того как сервер узнает, с кем он разговаривает, для проверки прав доступа нужно лишь просмотреть содержимое локальных таблиц или баз данных. По этой причине в данном разделе мы сосредоточимся на аутентификации.

Общая схема, используемая практически всеми протоколами аутентификации, состоит в следующем. Алиса желает установить защищенное соединение с Бобом или считающимся надежным KDC. Затем в разных направлениях передается еще несколько сообщений. При этом Труди может их перехватить, изменить и повторно воспроизвести, чтобы обмануть Алису и Боба или просто сорвать сделку.

Тем не менее, когда протокол завершает свою работу, Алиса уверена, что разговаривает с Бобом, а он — что разговаривает с Алисой. Кроме того, в большинстве протоколов собеседники могут установить секретный ключ сеанса (session key), чтобы использовать его в предстоящем обмене информацией. На практике, по соображениям производительности, поток данных кодируется с помощью алгоритма с симметричным ключом (обычно это AES), а шифрование с открытым ключом широко применяется для самих алгоритмов аутентификации и для установления ключа сеанса.

Существует несколько причин, по которым для каждого нового соединения используется новый, случайно выбранный ключ сеанса. Это снижение количества трафика, передаваемого с использованием закрытых и открытых ключей пользователя, уменьшение объема зашифрованного текста, который может получить злоумышленник, а также минимизация вреда, причиняемого в случае, если процесс даст сбой и дамп ядра (содержимое памяти) попадет не в те руки. Желательно, чтобы при этом в процессе хранился только ключ сеанса. Все постоянные ключи должны быть удалены после установления соединения.

Аутентификация на основе общего секретного ключа

Для нашего первого протокола аутентификации предположим, что у Алисы и Боба есть общий секретный ключ K_AB. О нем можно договориться лично или по телефону, но только не по незащищенной сети.

В основе данного протокола лежит принцип, актуальный для многих протоколов аутентификации: одна сторона отправляет другой случайное число, а та особым образом преобразует его и возвращает результат. Такие протоколы называют запросно-ответными (challenge-response). При рассмотрении протоколов аутентификации будут использоваться следующие условные обозначения:

A и B — Алиса и Боб;
R_i — запросы, где i — индекс отправителя;
K_i — ключи, где i — индекс владельца ключа;
K_S — ключ сеанса.

Последовательность сообщений данного протокола аутентификации с общим ключом показана на илл. 8.29. В первом сообщении Алиса отсылает свое удостоверение личности A Бобу (тем способом, который ему понятен). Боб, конечно, не знает, от кого пришло это сообщение — от Алисы или от Труди, поэтому он выбирает большое случайное число R_B и отправляет его в качестве запроса «Алисе» открытым текстом (сообщение 2). Затем Алиса шифрует это сообщение секретным ключом, общим для нее и Боба, и возвращает зашифрованный текст K_AB(R_B) в сообщении 3. Когда Боб видит это сообщение, он сразу понимает, что оно пришло именно от Алисы, поскольку Труди не располагает ключом K_AB и потому не может сформировать такое сообщение. Более того, поскольку запрос R_B выбирался случайным образом из большого пространства чисел (скажем, 128-битных), вероятность того, что Труди уже видела этот запрос и соответствующий ответ в одном из предыдущих сеансов, крайне низка. И вряд ли ей удастся подобрать правильный ответ на запрос наугад.

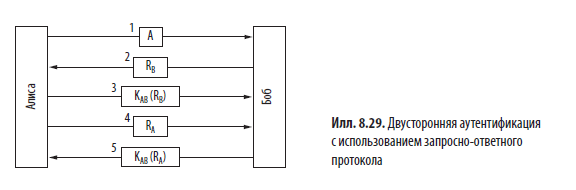
К этому моменту Боб уверен, что говорит с Алисой, однако она еще пока ни в чем не уверена. Алиса понимает, что Труди могла перехватить сообщение 1 и отправить обратно запрос RB. Возможно, Боба уже нет в живых. Чтобы узнать, с кем она говорит, Алиса выбирает случайное число R_A и отправляет его Бобу в виде открытого текста (сообщение 4). Когда Боб возвращает ответ K_AB(R_A), это убеждает Алису в том, что она говорит именно с ним. После этого они могут установить временный ключ сеанса K_S, который можно переслать друг другу, закодировав его все тем же общим ключом K_AB.

Число сообщений в этом протоколе можно сократить, объединив в каждом из них ответ на предыдущее сообщение с новым запросом (илл. 8.30). Здесь Алиса сама в первом же сообщении отправляет запрос Бобу. Отвечая на него, Боб помещает в это же сообщение свой запрос. Таким образом, вместо пяти сообщений понадобилось всего три.

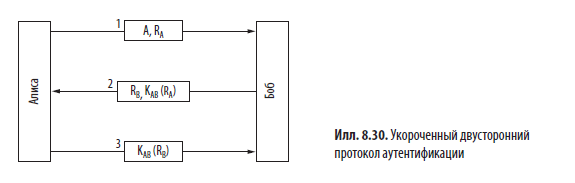
Можно ли утверждать, что этот протокол лучше изначального? С одной стороны, да, ведь он короче. Но, к сожалению, применять его не рекомендуется. При некоторых обстоятельствах Труди может атаковать этот протокол, используя зеркальную атаку (reflection attack). В частности, она может взломать его, если с Бобом можно открыть сразу несколько сеансов связи. Это вполне возможно, если Боб, скажем, является банком, который готов установить множество соединений с банкоматами одновременно.

Схема зеркальной атаки показана на илл. 8.31. Она начинается с того, что Труди, объявляя себя Алисой, отсылает запрос R_T. Боб, как обычно, отвечает своим собственным запросом R_B. Теперь, казалось бы, Труди в тупике. Что ей делать? Она ведь не знает K_AB(R_B).

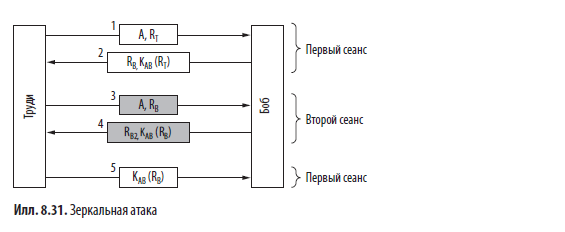
Однако Труди может открыть второй сеанс сообщением 3 и подать в качестве запроса Бобу его собственный запрос, взятый из сообщения 2. Боб спокойно шифрует его и отсылает обратно K_AB(R_B) в сообщении 4. Сообщения второго сеанса выделены в нашей схеме серым цветом. Труди получила нужную информацию, поэтому она завершает первый сеанс и прерывает второй. Теперь Боб уверен, что Труди — это Алиса, поэтому предоставляет ей доступ к банковским счетам Алисы и позволяет перевести деньги с ее текущего счета на секретный счет в швейцарском банке без малейших колебаний.

Мораль истории такова:

Разработать корректный протокол аутентификации гораздо сложнее, чем это может показаться.

Следующие четыре общих правила помогают разработчикам избежать распространенных ошибок.

1. Инициатор сеанса должен подтверждать свою личность прежде, чем это сделает отвечающая сторона. Это помешает злоумышленнику получить ценную для него информацию, прежде чем он подтвердит свою личность.

2. Следует использовать два раздельных общих секретных ключа: один для инициатора сеанса, а другой для отвечающего: K_AB и Kʹ_AB.

3. Инициатор и отвечающий должны выбирать запросы из разных наборов. Например, инициатор может использовать четные числа, а отвечающий — нечетные.

4. Протокол должен уметь противостоять атакам, при которых запускается второй параллельный сеанс, информация для которого извлекается из первого сеанса (или наоборот).

Если нарушается хотя бы одно из этих правил, протокол становится уязвимым. В приведенном примере игнорировались все четыре правила, что привело к разрушительным последствиям.
Вернемся к ситуации, показанной на илл. 8.29. Подвержен ли этот протокол зеркальным атакам? Точно сказать нельзя. Труди удалось справиться с нашим протоколом с помощью зеркальной атаки, поскольку он позволял запустить параллельный сеанс с Бобом и ввести его в заблуждение его собственным запросом. А что произойдет, если Алиса — обычный компьютер общего назначения, принимающий параллельные сеансы связи, а не человек? Посмотрим, что Труди сможет сделать.

Чтобы понять, каким образом Труди взламывает протокол, обратимся к илл. 8.32. Алиса объявляет свои идентификационные данные в сообщении 1. Труди это сообщение перехватывает и запускает собственный сеанс, отправляя сообщение 2 и прикидываясь Бобом. Здесь мы, как и раньше, изобразили серыми прямоугольниками сообщения второго сеанса. Алиса отвечает на сообщение 2: «Ты утверждаешь, что ты Боб? Докажи» (сообщение 3). Здесь Труди заходит в тупик: она не может подтвердить, будто она — это Боб.

Что же ей делать? Она возвращается к первому сеансу, где как раз наступает ее очередь отправки запроса. При этом отправляется запрос R_A, полученный в сообщении 3. Алиса любезно отвечает на это в сообщении 5, предоставляя тем самым Труди информацию, необходимую ей для создания сообщения 6 в сеансе 2. Теперь Труди может выбирать сеанс, так как она корректно ответила на запрос Алисы во втором сеансе. Сеанс 1 можно закрыть, отправить в сеансе 2 любое старое число и получить аутентифицированный сеанс связи с Алисой.

Но будучи перфекционисткой, Труди очень хочет показать, на что она способна. Вместо того чтобы отправить какое-нибудь старое число для завершения регистрации сеанса 2, она ждет, пока Алиса пришлет сообщение 7 (ее запрос для сеанса 1). Конечно, Труди понятия не имеет, как на него ответить, поэтому она вновь проводит зеркальную атаку, отправляя запрос R_A2 в сообщении 8. Алиса очень кстати шифрует R_A2 в сообщении 9. Труди переключается на сеанс 1 и отправляет Алисе нужное число в сообщении 10. Откуда она берет это число? Очевидно, из сообщения 9, пришедшего от Алисы. С этого момента Труди может гордиться тем, что у нее есть два полностью аутентифицированных сеанса связи с Алисой.

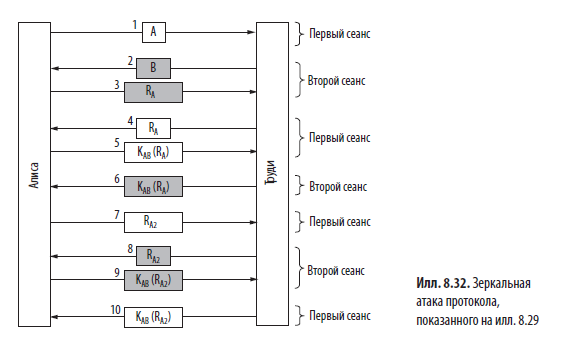
Эта атака приводит к несколько иному результату, нежели протокол с тремя сообщениями, который мы видели на илл. 8.31. На этот раз Труди удается установить сразу два аутентифицированных соединения с Алисой. В предыдущем примере одно такое соединение было установлено с Бобом. Опять же, если бы протокол удовлетворял всем четырем перечисленным требованиям, эту атаку можно было бы остановить. Различные типы атак и методы борьбы с ними подробно обсуждаются в работе Берда и др. (Bird et al., 1993). В ней вы также найдете описание планомерного построения протоколов, корректность которых можно доказать. Однако даже самый простой из них довольно сложен, поэтому далее мы рассмотрим другой класс протоколов, работающих ничуть не хуже.

Итак, новый протокол аутентификации показан на илл. 8.33 (Берд и др.; Bird et al., 1993). В нем используется код аутентификации сообщения на основе хеширования (Hashed Message Authentication Code, HMAC), гарантирующий целостность и подлинность сообщения. Простой и в то же время мощный код HMAC состоит из хеша на основе сообщения и общего ключа. Отправка HMAC вместе с сообщением не позволяет злоумышленнику изменить или подделать данные: смена любого бита приведет к неправильному хешу. Кроме того, сгенерировать корректный хеш невозможно, не располагая ключом. Коды HMAC привлекательны тем, что их можно очень эффективно генерировать (быстрее по сравнению с выполнением алгоритма SHA-2 с последующим применением к результатам алгоритма RSA).

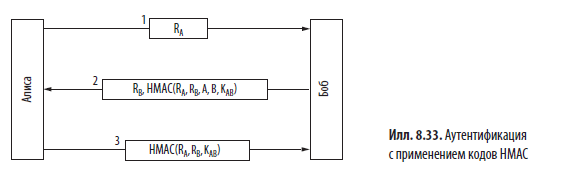
Для начала Алиса отправляет Бобу случайно выбранное число R_A (сообщение 1). Такие случайно выбранные числа, которые применяются в протоколах безопасности только один раз, принято называть нонсами (nonce); это сокращение от английского выражения «number used once» — «однократно используемое число». Боб при ответе выбирает собственный нонс RB и высылает его вместе с кодом HMAC. Этот код формируется путем построения структуры данных, состоящей из нонсов Алисы и Боба, их идентификаторов, а также общего секретного ключа K_AB. Затем вся эта структура с помощью хеш-функции (например, SHA-2) помещается в HMAC. После приема сообщения 2 у Алисы имеется значение R_A (она сама его выбрала), значение R_B, полученное в виде открытого текста, два идентификатора и секретный ключ KAB, который она и так знала. С помощью этих данных она может вычислить HMAC самостоятельно. Если он совпадает с кодом HMAC в сообщении, она убеждается, что говорит с Бобом. Ведь Труди не знает K_AB и, следовательно, не может угадать HMAC, который следует отослать. Алиса отправляет Бобу HMAC, содержащий только два нонса.

Вопрос: может ли Труди взломать такой протокол? Нет, поскольку она не может заставить ни одну из сторон зашифровать или хешировать выбранное ею значение, как было показано на илл. 8.31 и 8.32. Оба кода HMAC содержат значения, выбранные отправителем, и Труди не способна их контролировать.

Коды HMAC — далеко не единственный вариант применения этой идеи. Довольно распространенная альтернативная схема заключается в шифровании элементов данных последовательно, с помощью сцепления блоков шифра.

8.9.2. Установка общего ключа: протокол обмена ключами Диффи — Хеллмана

До сих пор мы подразумевали, что у Алисы и Боба есть общий секретный ключ. Теперь предположим, что такого ключа нет (поскольку до сих пор не разработана универсальная инфраструктура PKI для создания подписей и распространения сертификатов). Как же его установить? Алиса может позвонить Бобу и передать ключ по телефону, но Боб, скорее всего, спросит: «Как вы докажете, что вы — Алиса, а не Труди?» Можно попытаться организовать встречу, на которую каждый придет с паспортом, водительскими правами и тремя кредитными картами. Однако, будучи занятыми людьми, Алиса и Боб могут месяцами искать удобную дату. К счастью, совершенно незнакомые люди могут установить общий секретный ключ среди бела дня, даже если злоумышленник старательно записывает каждое сообщение.

Протокол, позволяющий устанавливать общий секретный ключ людям, которые друг друга не знают, называется протоколом обмена ключами Диффи — Хеллмана (Diffie — Hellman key exchange) (Diffie and Hellman, 1976). Он работает следующим образом. Алиса и Боб договариваются о двух больших простых числах, n и g, где (n – 1)/2 также является простым числом, кроме того, на число g накладываются некоторые дополнительные ограничения. Эти числа могут быть публичными, поэтому каждый просто устанавливает значения n и g и открыто сообщает о них собеседнику. Затем Алиса выбирает большое (например, двоичное 1024-разрядное) число x и держит его в тайне. Аналогично, Боб выбирает большое секретное число y.

Алиса запускает протокол обмена ключами, отправив Бобу сообщение (открытым текстом), содержащее (n, g, g^x mod n), как показано на илл. 8.34. Боб отвечает ей сообщением, содержащим g^y mod n. Алиса возводит присланное Бобом число в степень x и делит его по модулю на n, получая (g^y mod n)^x mod n. Боб выполняет аналогичные вычисления и получает (gx mod n)y mod n. Согласно законам модульной арифметики, оба вычисления должны быть равны g^xy mod n. Таким образом, как по мановению волшебной палочки, у Алисы и Боба появляется общий секретный ключ g^xy mod n.

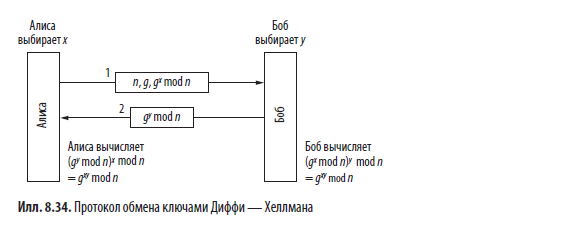
Конечно, Труди видит оба сообщения. Ей известны значения g и n из первого сообщения. Если бы она могла вычислить значения x и y, ей бы удалось получить секретный ключ. Беда в том, что, зная только g^x mod n, найти значение x очень трудно. На сегодняшний день неизвестен алгоритм вычисления дискретного логарифма модуля очень большого простого числа.

Для примера возьмем значения n = 47 и g = 3 (абсолютно нереалистичные). Алиса выбирает значение x = 8, а Боб — y = 10. Эти числа хранятся в секрете. Сообщение Алисы Бобу содержит числа (47, 3, 28), так как 3⁸ mod 47 = 28. Боб отвечает Алисе числом 17. Алиса вычисляет 17⁸ mod 47 и получает 4. Боб считает 28¹⁰ mod 47 и тоже получает 4. Таким образом, независимо друг от друга, Алиса и Боб определили, что значение секретного ключа равно 4. Чтобы найти ключ, Труди придется решить уравнение 3^x mod 47 = 28. Это можно сделать путем полного перебора при использовании небольших чисел, но не в случае чисел длиной в несколько сотен битов. Сегодня все известные алгоритмы требуют для этого вычисления гигантских временных затрат, даже при использовании сверхбыстрых суперкомпьютеров с десятками миллионов ядер.

Несмотря на всю элегантность алгоритма Диффи — Хеллмана, есть одна проблема: когда Боб получит три числа (47, 3, 28), как удостовериться в том, что их отправила Алиса, а не Труди? Нет никакого способа узнать это. К сожалению, Труди может воспользоваться этим, чтобы обмануть Алису и Боба (илл. 8.35). Пока Алиса и Боб устанавливают значения x и y, Труди выбирает свое случайное число z. Алиса отсылает Бобу сообщение 1. Труди перехватывает его и вместо него отправляет Бобу сообщение 2, используя правильные значения g и n (которые передавались открытым текстом), но со своим значением z вместо x. Она также отсылает сообщение 3 обратно Алисе. Позднее Боб отправляет Алисе сообщение 4, которое Труди снова перехватывает и хранит у себя.

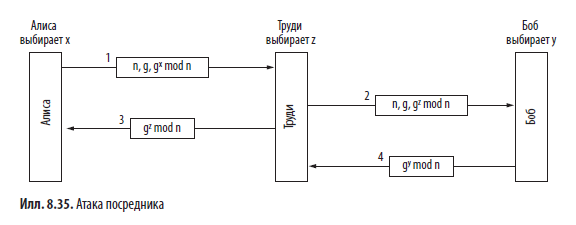
Теперь все занимаются вычислением остатков от деления. Алиса вычисляет значение секретного ключа g^xz mod n. Те же самые подсчеты производит Труди (для общения с Алисой). Боб вычисляет g^yz mod n, что также делает и Труди (для общения с Бобом). Думая, что она общается с Бобом, Алиса устанавливает ключ сеанса (с Труди), и точно так же поступает Боб. Каждое сообщение, отправляемое Алисой в шифрованном сеансе, перехватывается Труди, сохраняется, изменяется, если нужно, и отсылается (по желанию Труди) Бобу. То же самое происходит в обратном направлении. Труди видит все сообщения и может менять их по своему усмотрению, в то время как Алиса и Боб полагают, что у них имеется защищенный канал для связи друг с другом. Подобные действия злоумышленника называются «атакой посредника» или атакой типа «человек посередине» (man-in-the-middle attack).

Более подробно с книгой можно ознакомиться на сайте издательства.