Новости
03.08.2023
Книга «Data Science в действии»
При этом читателям необходимо знать азы программирования на Python. Умений, полученных в ходе самостоятельного изучения, должно быть достаточно для проработки примеров из книги. Математических знаний выше школьного курса тригонометрии не потребуется.
10.2. K-СРЕДНИЕ:
АЛГОРИТМ КЛАСТЕРИЗАЦИИ ДЛЯ ГРУППИРОВКИ ДАННЫХ ПО K ЦЕНТРАЛЬНЫХ ГРУПП
Алгоритм K-средних предполагает, что входные точки данных сосредотачиваются вокруг K разных центров. Координаты каждого центра подобны скрытому яблочку, окруженному разбросанными точками данных. Задача данного алгоритма — выявить эти скрытые центральные координаты.
Мы инициализируем K-средние, начав с выбора K, представляющего количество искомых центральных координат. При анализе мишени K равнялось 2, хотя по факту может равняться любому целому числу. Алгоритм случайно выбирает K точек данных, которые начинают рассматриваться как истинные центры. После этого алгоритм итеративно обновляет выбранные центральные точки, которые аналитики называют центрами масс. В рамках одной итерации каждая точка данных приписывается к ближайшему центру, в результате чего формируются K групп.. Затем центр каждой группы обновляется. При этом он оказывается равен среднему координат его группы. Если этот процесс повторять достаточно долго, то средние группы сойдутся к K репрезентативным центрам (рис. 10.6). Такое схождение гарантируется математически, однако необходимое для этого количество итераций заранее узнать нельзя. Общепринятый прием заключается в том, чтобы прекращать повторения, когда ни один из вновь вычисленных центров не отклоняется значительно от своего предшественника.
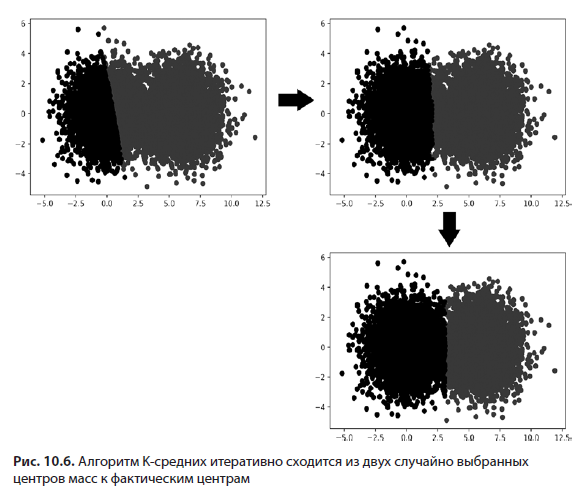
Метод K-средних имеет и ограничения. Этот алгоритм основывается на нашем знании K, то есть количества искомых кластеров. Зачастую подобная информация оказывается недоступной. К тому же, хотя этот метод обычно и находит разумные центры, он не дает математической гарантии, что они окажутся наилучшими для рассматриваемых данных. Временами он возвращает нелогичные или неоптимальные группы из-за неудачного выбора случайных центров масс на этапе инициализации. Наконец, этот метод предполагает, что кластеры данных фактически сосредоточены вокруг K центральных точек, хотя чуть позже мы узнаем, что это предположение не всегда верно.
10.2.1. Кластеризация по методу K-средних с помощью scikit-learn
При удачной реализации алгоритм K-средних выполняется за вполне приемлемое время. Подобную быстродействующую реализацию может обеспечить внешняя библиотека scikit-learn. Она представляет собой невероятно популярный инструмент машинного обучения, построенный на базе NumPy и SciPy. Эта библиотека несет в себе различные фундаментальные алгоритмы классификации, регрессии и кластеризации, включая, конечно же, метод K-средних. Для начала мы ее установим (листинг 10.8), после чего импортируем необходимый для кластеризации класс KMeans.
ПРИМЕЧАНИЕ
Для установки scikit-learn выполните из терминала pip install scikit-learn.
Листинг 10.8. Импорт KMeans из scikit-learn
from sklearn.cluster import KMeans
Применить KMeans к нашим darts будет просто (листинг 10.9). Сначала нужно выполнить KMeans(n_clusters=2), что приведет к созданию объекта cluster_model, способного найти два центра. Затем можно будет запустить сам алгоритм вызовом cluster_model.fit_predict (darts). Этот метод вернет массив assigned_bulls_eyes, хранящий индекс центра каждой мишени.
Листинг 10.9. Кластеризация методом K-средних с помощью scikit-learn

Теперь для проверки результатов раскрасим дротики согласно принадлежности к тому или иному кластеру (листинг 10.10; рис. 10.7).
Листинг 10.10. Раскрашивание точек данных на основе принадлежности к кластеру
for bs_index in range(len(bulls_eyes)):
selected_darts = [darts[i] for i in range(len(darts))
if bs_index == assigned_bulls_eyes[i]]
x_coordinates, y_coordinates = np.array(selected_darts).T
plt.scatter(x_coordinates, y_coordinates,
color=['g', 'k'][bs_index])
plt.show()
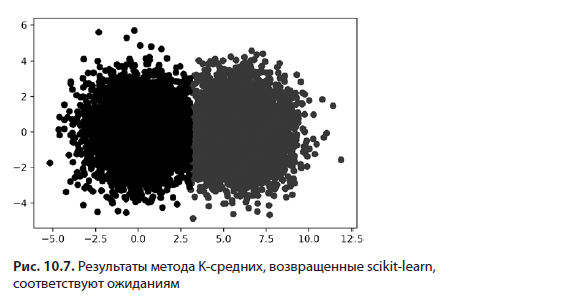
Наша модель кластеризации обнаружила в данных центры масс.. Теперь эти центры масс можно использовать для анализа новых точек данных, которые модель еще не видела. Выполняя cluster_model.predict([x, y]), мы присваиваем центр масс точке данных, определяемой координатами x и y (листинг 10.11). Для кластеризации двух новых точек данных применяется метод predict.
Листинг 10.11. Кластеризация новых данных при помощи cluster_model
new_darts = [[500, 500], [-500, -500]]
new_bulls_eye_assignments = cluster_model.predict(new_darts)
for i, dart in enumerate(new_darts):
bulls_eye_index = new_bulls_eye_assignments[i]
print(f"Dart at {dart} is closest to bull's-eye {bulls_eye_index}")
Dart at [500, 500] is closest to bull's-eye 0
Dart at [-500, -500] is closest to bull's-eye 1
10.2.2. Выбор оптимального K методом локтя
Алгоритм K-средних опирается на входное значение K, что может стать серьезной помехой, когда количество подлинных кластеров в данных заранее неизвестно.. Но мы все же можем подобрать подходящее значение K, используя технику под названием «метод локтя».
Если K = 1, тогда инерция будет равна сумме всех возведенных в квадрат расстояний до среднего набора данных. Это значение, как говорилось в главе 5, прямо пропорционально дисперсии. В свою очередь, дисперсия является мерой рассеяния. Таким образом, если K = 1, инерция является оценочным показателем рассеяния. Это свойство работает, даже если K > 1. По сути, инерция приблизительно показывает рассеяние вокруг K вычисленных средних.
Оценивая рассеяние, можно определить, является ли наше значение K излишне большим или малым. Представим, что установили его равным 1. Не исключено, что многие точки данных окажутся размещены очень далеко от одного центра.. Рассеяние и инерция получатся большими. По мере увеличения K в направлении более разумного числа возникающие дополнительные центры приведут к уменьшению инерции.. В конечном итоге, если излишне увлечься и установить K равным общему количеству точек, каждая из них попадет в собственный кластер. При этом рассеяние полностью исчезнет, и инерция окажется равна нулю (рис. 10.8).
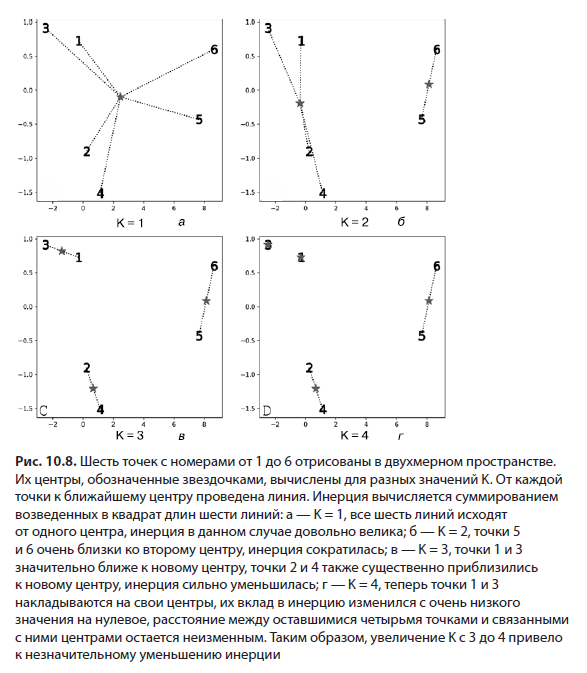
Одни значения инерции излишне велики, другие, наоборот, слишком малы, но где-то между этими крайностями находится то самое верное значение. Как же его отыскать?
Далее мы проработаем решение этого вопроса, начав с графического отображения инерции набора данных с мишеней для большого диапазона значений K (листинг 10.12; рис. 10.9). Инерция автоматически вычисляется для каждого scikit-learn-объекта KMeans. Обратиться к этому сохраненному значению можно через атрибут модели inertia_.
Листинг 10.12. Построение графика инерции для K-средних
k_values = range(1, 10)
inertia_values = [KMeans(k).fit(darts).inertia_
for k in k_values]
plt.plot(k_values, inertia_values)
plt.xlabel('K')
plt.ylabel('Inertia')
plt.show()
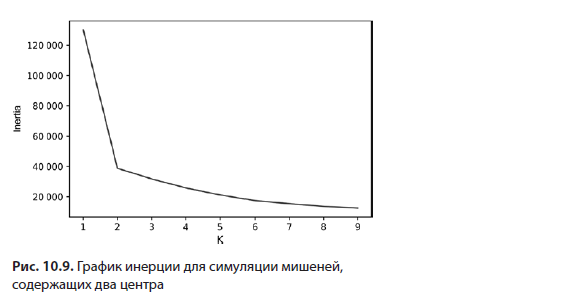
Сгенерированный график напоминает руку, согнутую в локте, который указывает на значение K, равное 2. Как нам уже известно, это K точно охватывает два центра, которые мы предварительно заложили в набор данных.
Продолжит ли этот подход работать, если количество представленных центров увеличить? Это можно выяснить, добавив в симуляцию еще один. После увеличения числа кластеров до трех мы повторно сгенерируем график инерции (листинг 10.13; рис. 10.10).
Листинг 10.13. Построение графика инерции для симуляции с тремя мишенями
new_bulls_eye = [12, 0]
for _ in range(5000):
x = np.random.normal(new_bulls_eye[0], variance ** 0.5)
y = np.random.normal(new_bulls_eye[1], variance ** 0.5)
darts.append([x, y])
inertia_values = [KMeans(k).fit(darts).inertia_
for k in k_values]
plt.plot(k_values, inertia_values)
plt.xlabel('K')
plt.ylabel('Inertia')
plt.show()

Добавление третьего центра дает новую форму локтя, чей нижний изгиб указывает на значение K, равное 3. По сути, этот график прослеживает рассеяние, включаемое каждым увеличением K. Быстрое увеличение инерции между последовательными значениями K подразумевает, что разбросанные точки данных должны быть приписаны к более плотному кластеру. По мере уплощения кривой инерции уменьшение этого показателя постепенно утрачивает свое влияние. Этот переход от вертикального уклона к более плавному углу ведет к появлению на графике формы локтя. Позицию этого локтя можно применить для выбора подобающего K в алгоритме K-средних.
Использование метода локтя — полезный эвристический прием, но он не обязательно сработает в каждом случае. В определенных условиях уровни локтя при переборе нескольких значений K уменьшаются медленно, что усложняет выбор единственно верного количества кластеров.
ПРИМЕЧАНИЕ
Существуют и более мощные методы выбора K, например коэффициент «силуэт», который учитывает расстояние каждой точки до соседних кластеров. Подробный разбор этого подхода выходит за рамки данной книги, но вы вполне можете изучить принцип его работы самостоятельно, используя метод sklearn.metrics.silhouette_score.
Метод локтя неидеален, но вполне пригоден, когда данные центрированы вокруг K раздельных средних. Естественно, это подразумевает, что наши кластеры данных различаются на основе центральности.. Однако во многих случаях они различаются на основе плотности распределения точек данных в пространстве. Далее мы рассмотрим этот принцип организации регулируемых плотностью кластеров, которые не зависят от центральности.
МЕТОДЫ КЛАСТЕРИЗАЦИИ ПО K-СРЕДНИМ
- k_means_model = KMeans(n_clusters=K)— создает модель K-средних для поиска K различных центров масс. Эти центры масс необходимо сопоставить с входными данными.
- clusters = k_means_model.fit_predict(data) — выполняет алгоритм K-средних для входных данных, используя инициализированный объект KMeans. Возвращаемый массив clusters содержит ID кластеров в диапазоне от 0 до K. ID кластера data[i] равен clusters[i].
- clusters = KMeans(n_clusters=K).fit_predict(data) — выполняет алгоритм K-средних в одной строке кода, возвращая полученные кластеры.
- new_clusters = k_means_model.predict(new_data) — находит ближайшие центры масс для ранее неизвестных данных, используя имеющиеся центры масс в оптимизированном данными объекте KMeans.
- inertia = k_means_model.inertia_ — возвращает инерцию, связанную с оптимизированным данными объектом KMeans.
- inertia = KMeans(n_clusters=K).fit(data).inertia_ — выполняет алгоритм K-средних в одной строке кода, возвращая полученную инерцию.
Более подробно с книгой можно ознакомиться на сайте издательства.





Комментарии: 0
Пока нет комментариев