Новости

Для кого эта книга

Алгоритмы в истории. Русское крестьянское умножение

Изучение таблицы умножения многим запомнилось как особенно трудный этап образования. Дети спрашивают своих родителей, почему так важно учить таблицу умножения, и родители обычно отвечают, что без этого нельзя умножать. Как же они ошибаются! Существует русское крестьянское умножение (Russian Peasant Multiplication, RPM) — метод, позволяющий перемножать большие числа, обходясь без знания большей части таблицы умножения.

Происхождение RPM остается неясным. Древнеегипетский свиток, называемый папирусом Ринда, содержит разновидность этого алгоритма. Некоторые историки предложили гипотезы (большей частью неубедительные) о том, как метод мог перейти от древнеегипетских ученых к крестьянам необъятной российской глубинки. Как бы то ни было, алгоритм RPM весьма интересен.

RPM вручную

Представьте, что хотите умножить 89 на 18. RPM работает так: сначала нарисуйте два расположенных рядом друг с другом столбца. Первый называется столбцом деления, сначала в нем находится число 89. Второй называется столбцом умножения, и в исходном состоянии в нем находится число 18 (табл. 2.1).

Начнем с заполнения столбца деления. Для каждой его строки берем предыдущее значение и делим его на 2, остаток при этом игнорируется. Например, при делении 89 на 2 мы получаем 44 с остатком 1, поэтому во второй строке столбца деления записывается число 44 (табл. 2.2).

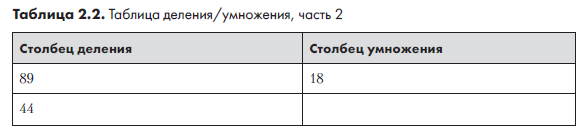
Деление на 2 продолжается, пока не будет получен результат 1. При этом каждый раз остаток отбрасывается, а результат записывается в следующую строку. Половина от 44 равна 22, половина от 22 равна 11, половина от 11 (с потерей остатка) равна 5, затем 2, затем 1. Записав эти числа в столбец деления, мы получаем табл. 2.3.

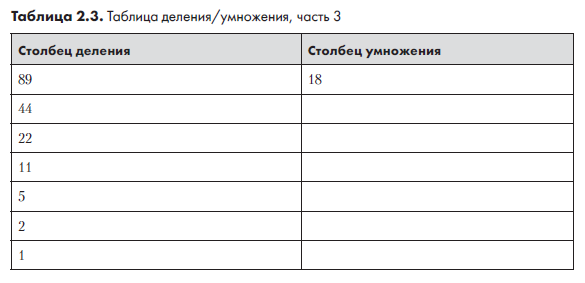
Столбец деления готов. Каждый элемент столбца умножения равен удвоенному предыдущему элементу. Так как 18 × 2 = 36, вторая строка столбца умножения содержит 36 (табл. 2.4).

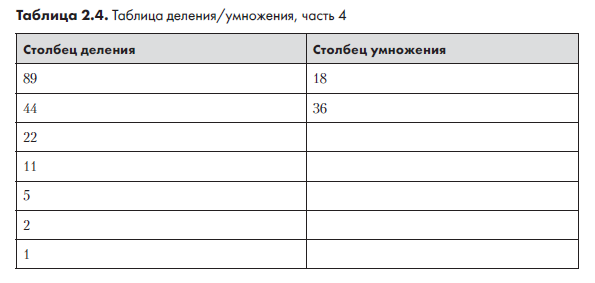
Далее мы продолжаем добавлять элементы в столбец умножения по тому же правилу: предыдущее значение удваивается. Это продолжается до тех пор, пока столбец умножения не сравняется по количеству элементов со столбцом деления (табл. 2.5).

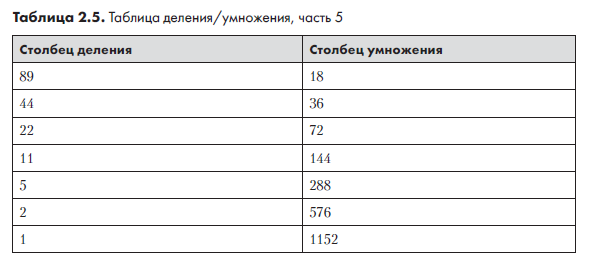
На следующем шаге из таблицы удаляются все строки, у которых столбец деления содержит четное число. Результат показан в табл. 2.6.

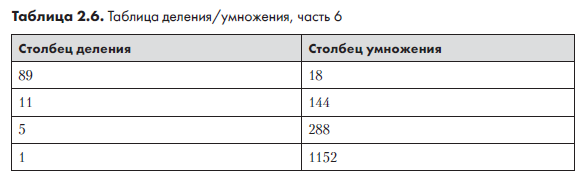
Остается сложить все оставшиеся числа в столбце умножения. Результат равен 18 + 144 + 288 + 1152 = 1602. Правильность ответа можно проверить на калькуляторе: 89 × 18 = 1602. Умножение было реализовано с помощью операций деления надвое, удвоения и сложения, и нам не пришлось запоминать большую часть скучной таблицы умножения, которую так не любят дети.

Чтобы понять, почему работает этот метод, попробуйте переписать столбец умножения в виде множителей 18 — умножаемого числа (табл. 2.7).

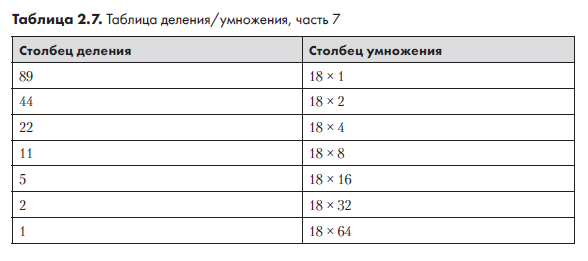
В столбце умножения следует серия множителей 1, 2, 4, 8 и т. д. до 64. Все эти числа являются степенями 2, и их также можно записать в виде 2⁰, 2¹, 2² и т. д. Когда мы вычисляем итоговую сумму (складываем строки столбца умножения, у которых столбец деления содержит нечетное значение), в действительности вычисляется следующая сумма:

18 × 2⁰ + 18 × 2³ + 18 × 2⁴ + 18 × 2⁶ = 18 × (2⁰ + 2³ + 2⁴ + 2⁶) = 18 × 89.

Работа RPM зависит от следующего факта:

(2⁰ + 2³ + 2⁴ + 2⁶) = 89.

Внимательно присмотревшись к столбцу деления, можно понять, почему данное уравнение истинно. Этот столбец тоже можно записать в степенях 2 (табл. 2.8).

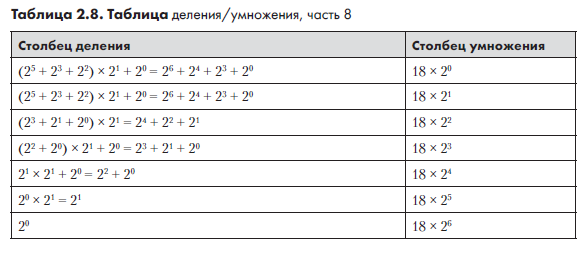
При этом проще начать с наименьшего числа и двигаться снизу вверх. Стоит напомнить, что 2⁰ = 1, а 2¹ = 2. В каждой строке значение умножается на 2¹, а в строках, в которых делимое число нечетно, также добавляется 2⁰. При продвижении по строкам выражение начинает все больше напоминать наше уравнение. К моменту достижения верхней строки таблицы мы получаем выражение, которое упрощается в точности до 2⁶ + 2⁴ + 2³ + 2⁰.

Если мы пронумеруем строки столбца деления (верхняя строка обозначается как строка 0, затем 1, 2 и вплоть до нижней строки 6), то увидим, что нечетные значения в столбце деления содержатся в строках 0, 3, 4 и 6. Теперь заметим важнейшую закономерность: номера этих строк в точности совпадают с показателями степеней в найденном нами выражении для 89: 2⁶ + 2⁴ + 2³ + 2⁰. И это совпадение не случайно; способ построения столбца деления означает, что нечетные значения всегда находятся в строках, номера которых равны показателям степени в сумме степеней 2, равной нашему исходному числу. Когда мы вычисляем сумму элементов столбца умножения с этими индексами, мы фактически суммируем произведения 18 на степени 2, дающие в сумме 89, поэтому результат будет равен 89 × 18.

Почему же эта схема работает? В действительности RPM является алгоритмом внутри алгоритма. Сам столбец деления может считаться реализацией алгоритма, который находит сумму степеней 2, равную числу в первой ячейке столбца. Сумма степеней 2 также называется двоичным разложением числа 89. Двоичная система представляет собой альтернативную схему записи чисел с использованием только 0 и 1; она стала играть особенно важную роль в последние десятилетия, поскольку компьютеры хранят информацию в двоичном виде. В двоичной записи число 89 записывается в виде 1011001, с единицами в нулевой, третьей, четвертой и шестой позиции (справа налево); номера позиций соответствуют номерам нечетных строк столбца деления, а также степеням нашего уравнения. 1 и 0 в двоичном представлении можно рассматривать как коэффициенты в сумме степеней 2. Например, двоичное число 100 интерпретируется следующим образом:

1 × 2² + 0 × 2¹ + 0 × 2⁰

или 4 в обычной (десятичной) записи. Двоичное число 1001 интерпретируется так:

1 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰.

или 9 в обычной записи. После выполнения мини-алгоритма для получения двоичного разложения 89 можно легко выполнить полный алгоритм и завершить процесс умножения.

Реализация RPM на Python

Реализация RPM на Python получается относительно простой. Допустим, вы хотите умножить два числа; назовем их n1 и n2. Для начала откроем сценарий Python и определим эти переменные:

n1 = 89
n2 = 18

На следующем шаге начнем строить столбец деления. Как упоминалось выше, он начинается с одного из перемножаемых чисел:

halving = [n1]

Следующий элемент равен halving[0]/2 с игнорированием остатка. В Python для округления можно воспользоваться функцией math.floor(). Функция просто находит ближайшее целое число, которое меньше заданного. Например, вторая строка столбца деления вычисляется так:

import math
print(math.floor(halving[0]/2))

Выполнив этот код в Python, вы увидите, что результат равен 44.

Программа перебирает все строки столбца деления, при каждой итерации цикла находит следующее значение в данном столбце и останавливается при достижении 1:

while(min(halving) > 1):
       halving.append(math.floor(min(halving)/2))

В цикле метод append() используется для конкатенации. При каждой итерации цикла while вектор деления объединяется с половиной его последнего значения, при этом функция math.floor() используется для игнорирования остатка.

Со столбцом умножения делаем то же самое: мы начинаем с 18 и запускаем цикл. При каждой итерации цикла в столбец умножения добавляется удвоенное последнее значение. Цикл останавливается, когда длина этого столбца достигнет длины столбца деления:

doubling = [n2]
while(len(doubling) < len(halving)):
       doubling.append(max(doubling) * 2)

Наконец, эти два столбца помещаются в кадр данных half_double:

import pandas as pd
half_double = pd.DataFrame(zip(halving,doubling))

Здесь импортируется модуль Python pandas. Он упрощает работу с таблицами. В данном случае используется команда zip, которая соединяет halving с doubling подобно тому, как застежка-«молния» соединяет две полы куртки. Два набора чисел halving и doubling создаются как независимые списки, а после соединения и преобразования в кадр данных pandas сохраняются в таблице в виде двух параллельных столбцов, как показано выше в табл. 2.5. Поскольку столбцы выровнены и соединены, мы можем обратиться к любой строке табл. 2.5 (например, третьей) и получить всю строку данных, включающую элементы из halving и doubling (2 и 72). Возможность обращаться к этим строкам и работать с ними позволяет легко удалить ненужные строки, как было сделано с табл. 2.5 для преобразования ее в табл. 2.6.

Теперь необходимо удалить строки с четными значениями в столбце деления. Для проверки четности можно воспользоваться оператором % языка Python, возвращающим остаток от деления. Если число x нечетно, то x%2 будет равно 1. Следующая строка оставляет в таблице только те строки, у которых значение в столбце деления является нечетным:

half_double = half_double.loc[half_double[0]%2 == 1,:]

В данном случае для отбора только интересующих нас строк используется функциональность loc модуля pandas. При использовании loc отбираемые строки и столбцы заключаются в квадратные скобки ([]). В них нужные строки и столбцы перечисляются через запятую: [строка, столбец]. Например, если вам нужна строка с индексом 4 и столбец с индексом 1, то можно прибегнуть к записи half_double.loc[4,1]. При этом ваши возможности не ограничиваются простым указанием индексов. Можно записать логический шаблон для отбора нужных строк: нас интересуют все строки, где halving содержит нечетное значение. В нашей логике столбец halving обозначается half_double[0], то есть столбец с индексом 0. Нечетность определяется условием %2 == 1. Наконец, чтобы указать, что нам нужны все столбцы, после запятой ставится двоеточие — это сокращение означает, что нам нужны все столбцы.

Остается вычислить сумму оставшихся элементов doubling:

answer = sum(half_double.loc[:,1])

Здесь снова используется loc. Квадратные скобки указывают, что нам нужны все строки, для чего снова применяется сокращение с двоеточием. Мы указываем, что нам нужен вектор doubling (столбец с индексом 1 после запятой). Обратите внимание: рассмотренный нами пример 89 × 18 можно было бы реализовать быстрее и проще, если бы вместо этого вычислялось произведение 18 × 89. То есть если бы значение 18 находилось в столбце halving, а значение 89 — в столбце doubling. Попробуйте самостоятельно реализовать это улучшение. В общем случае RPM работает быстрее, если меньший множитель находится в столбце деления, а больший — в столбце умножения.

Тому, кто уже запомнил таблицу умножения, алгоритм RPM может показаться бесполезным. Но помимо исторической ценности, его стоит изучить по нескольким причинам. Прежде всего, алгоритм показывает, что даже такую сухую операцию, как умножение чисел, можно выполнять по-разному, и в ней есть место для творческого подхода. Даже если вы освоили один алгоритм для какой-то задачи, это не означает, что он является единственным или лучшим алгоритмом для своей цели, — держите свой разум открытым для новых и, возможно, лучших решений.

RPM работает медленно, но требует меньших начальных усилий, поскольку вам не нужно заранее знать большую часть таблицы умножения. Иногда полезно пойти на небольшие потери скорости ради снижения затрат памяти, и этот баланс между скоростью/затратами памяти становится важным фактором во многих ситуациях с проектированием и реализацией алгоритмов.

Как и многие лучшие алгоритмы, RPM также подчеркивает отношения между разрозненными, на первый взгляд, идеями. Может показаться, что двоичное разложение представляет интерес только для создателей транзисторов, но бесполезно для обывателя или профессионального программиста. Однако RPM демонстрирует глубокую связь между двоичным разложением числа и удобным способом умножения, требующим минимальных знаний таблицы умножения. Это еще одна причина, по которой всегда следует продолжать учиться: никогда не знаешь, когда бесполезный, на первый взгляд, факт может оказаться основой для мощного алгоритма.