Новости

Крупномасштабные алгоритмы

Крупномасштабные алгоритмы, или алгоритмы решения задач большой размерности (large-scale algorithms), предназначены для решения невероятно сложных задач. Они нуждаются в нескольких механизмах выполнения ввиду крупных объемов данных и серьезных требований к обработке. В этой главе мы рассмотрим типы алгоритмов, требующих параллельного выполнения, и обсудим распараллеливание. Далее мы познакомимся с архитектурой CUDA и выясним, как ускорять алгоритмы с помощью одного или нескольких графических процессоров (GPU). Мы научимся изменять алгоритм таким образом, чтобы эффективно использовать мощность GPU. Наконец, коснемся кластерных вычислений. Мы узнаем, как наборы данных RDD в Apache Spark используются для чрезвычайно быстрой параллельной реализации стандартных алгоритмов.

ВВЕДЕНИЕ В КРУПНОМАСШТАБНЫЕ АЛГОРИТМЫ

Людям нравится преодолевать трудности. На протяжении веков мы придумываем инновационные способы решения сложных проблем. От предсказания района нашествия саранчи и до вычисления наибольшего простого числа, методы поиска ответов на трудные вопросы продолжают развиваться. С появлением компьютеров мы получили новый мощный способ решения сложных задач.

Определение эффективного крупномасштабного алгоритма

Хорошо продуманный крупномасштабный алгоритм обладает следующими двумя характеристиками:

• Он справляется с гигантским объемом данных и обширными требованиями к обработке, наилучшим образом используя доступные ресурсы.
• Он масштабируется. По мере усложнения проблемы алгоритм просто задействует больше ресурсов.

Наиболее практичный способ реализации крупномасштабных алгоритмов — стратегия «разделяй и властвуй». Это разбиение крупной задачи на более мелкие, которые решаются независимо друг от друга.

Терминология

Рассмотрим некоторые термины, используемые для количественной оценки качества крупномасштабных алгоритмов.

Задержка

Задержка (latency) — это общее время, необходимое для выполнения одного вычисления. Допустим, C1 — это одно вычисление, которое начинается в t1 и заканчивается в t2, тогда можно сказать следующее:

Latency = t2 – t1.

Пропускная способность

В контексте параллельных вычислений пропускная способность (throughput) — это количество отдельных вычислений, которые могут выполняться одновременно. Например, если при t1 можно выполнить четыре одновременных вычисления, C1, C2, C3 и C4, то пропускная способность равна четырем.

Полоса бисекции сети

Полоса пропускания между двумя равными частями сети называется полосой бисекции сети (network bisection bandwidth). Это самый важный параметр, влияющий на эффективность распределенных вычислений. При недостаточной полосе бисекции скорость соединения будет медленной. Таким образом, будет потеряно преимущество, полученное благодаря наличию нескольких механизмов выполнения.

Эластичность

Способность инфраструктуры среагировать на внезапное увеличение требований к обработке и выделить большее количество ресурсов называется эластичностью.

Три гиганта облачных вычислений, Google, Amazon и Microsoft, способны обеспечить высокоэластичную инфраструктуру. Их общий пул ресурсов огромен, и существует очень мало компаний, способных добиться такой же эластичности.

Если инфраструктура эластична, она способна создать масштабируемое решение для задачи.

РАЗРАБОТКА ПАРАЛЛЕЛЬНЫХ АЛГОРИТМОВ

Важно отметить, что параллельные алгоритмы не являются панацеей. Даже лучшие параллельные архитектуры могут не обеспечить ожидаемой производительности. Рассмотрим закон, который широко применяется для разработки параллельных алгоритмов, — закон Амдала.

Закон Амдала

Джин Амдал был одним из первооткрывателей параллельной обработки в 1960-х годах. Он предложил закон, который актуален до сих пор. Закон Амдала может служить основой для понимания различных компромиссов, связанных с разработкой решений для параллельных вычислений.

Согласно закону Амдала, не все части вычислительного процесса могут выполняться параллельно. Всегда будет последовательная часть процесса, которая не может быть распараллелена.

Рассмотрим конкретный пример. Предположим, необходимо прочитать большое количество файлов, хранящихся на компьютере, и обучить модель МО, используя полученные данные.
Назовем этот процесс P. Очевидно, что P можно разделить на два подпроцесса:

• P1: просканировать файлы в каталоге, создать список имен файлов, соответствующих входному файлу, и передать список дальше.
• P2: прочитать файлы, создать пайплайн обработки данных, обработать файлы и обучить модель.

Анализ последовательного процесса

Время выполнения P представлено как Tseq(P). Время выполнения P1 и P2 представлено как Tseq(P1) и Tseq(P2). Очевидно, что при работе на одной ноде мы будем наблюдать следующее:

• P2 не может начать работу до завершения P1. Это представляется как P1 — >P2.
• Tseq(P) = Tseq(P1) + Tseq(P2).

Предположим, что запуск P на одной ноде в целом занимает 11 секунд. Из них выполнение P1 занимает 2 секунды, а выполнение P2 — 9 секунд. Работа алгоритма показана на следующей схеме (рис. 13.1).

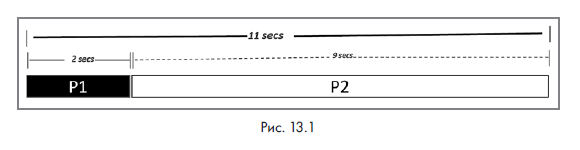
Важно отметить, что P1 является последовательным по своей природе. Этот процесс невозможно ускорить, сделав его параллельным. Вместе с тем P2 легко делится на подзадачи, которые могут выполняться одновременно. Их параллельный запуск ускоряет работу процесса.

Основным преимуществом облачных вычислений является наличие большого пула ресурсов, и многие из них используются параллельно. План применения этих ресурсов для конкретной задачи называется планом выполнения. Закон Амдала используется для тщательного выявления ограничений задачи и пула ресурсов.

Анализ параллельного выполнения

Если используется более одной ноды для ускорения P, это повлияет на P2 только с коэффициентом s > 1:

Ускорение процесса P можно легко рассчитать следующим образом:

Отношение распараллеливаемой части процесса к его общему количеству представлено b и рассчитывается так:

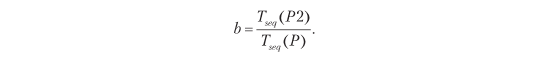
Например, в предыдущем сценарии b = 9/11 = 0.8182.

Упрощение этих уравнений даст нам закон Амдала:

Итак‚ мы имеем следующее:

• P — это общий процесс;
• b — отношение распараллеливаемой части P;
• s — ускорение, достигнутое в распараллеливаемой части P.

Предположим, процесс P запускается на трех параллельных нодах:

• P1 является последовательным и не может быть сокращен с помощью параллельных нод. Он по-прежнему длится 2 секунды.
• P2 теперь занимает 3 секунды вместо 9.

Таким образом, общее время, затрачиваемое процессом P, сокращается до 5 секунд, как показано на следующей диаграмме (рис. 13.2).

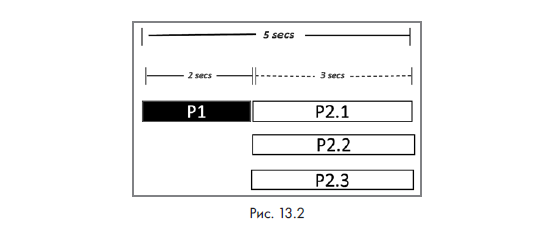
Вычислим также:

• np = количество процессоров = 3;
• b = параллельная часть = 9/11 = 81,82 %;
• s = ускорение = 3.

Теперь взглянем на типичный график, объясняющий закон Амдала (рис. 13.3).

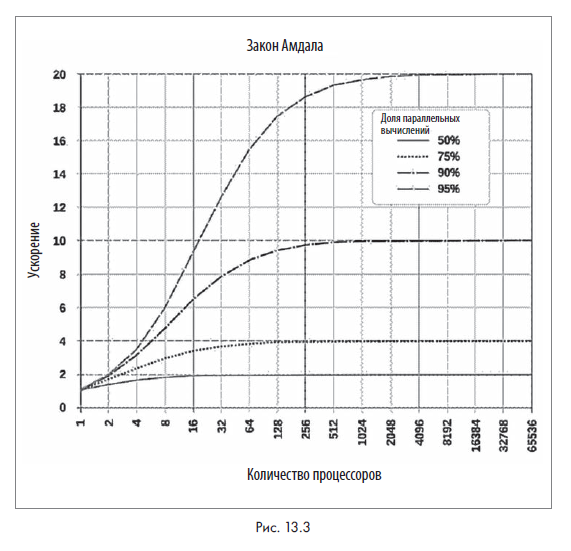
На этой диаграмме график строится между s и np для разных значений b.

Гранулярность задачи

При распараллеливании алгоритма большая задача делится на несколько параллельных подзадач. Их оптимальное количество не всегда очевидно. Если подзадач слишком мало, параллельные вычисления не принесут особой пользы; слишком большое количество подзадач чересчур увеличит затраты ресурсов. Эта проблема называется гранулярностью задачи.

Балансировка нагрузки

В параллельных вычислениях за выбор ресурсов для выполнения задачи отвечает планировщик. Оптимальной балансировки нагрузки достичь сложно, а при ее отсутствии ресурсы используются не в полной мере.

Проблема расположения

При параллельной обработке не рекомендуется перемещать данные. По возможности их следует обрабатывать в той ноде, в которой они находятся. В противном случае качество распараллеливания снижается.

Запуск параллельной обработки на Python

Самый простой способ запустить параллельную обработку на Python — это клонировать текущий процесс, который запустит новый параллельный процесс, называемый дочерним.

Программисты Python (хотя они и не биологи) создали собственный процесс клонирования. Как и в случае с клонированной овцой, клонированный процесс является точной копией исходного процесса.

Подробнее с книгой можно ознакомиться в нашем каталоге.